Grand Oral : Comment prévoir les cours de bourse avec ChatGPT et les séries de Fourier

Les Séries de Fourier sont un outil mathématique qu’il est maintenant très facile d’implémenter en Python avec ChatGPT. Dans ce post, je vais vous montrer comment on peut se servir de la décomposition en séries de Fourier pour tenter de prévoir les cours de bourse. Un bon sujet pour le Grand Oral de Maths ! Allez ! On commence !

La décomposition des signaux en séries de Fourier

Un grand nombre de courbes peuvent être approchées par une décomposition en séries de Fourier. Par exemple, vous connaissez sans doute les développements limités. Les DL approchent une courbe à un point donné (ou une asymptote).

Ainsi, les séries de Fourier sont un moyen d’approcher une courbe sur tous ses points. Mais d’abord, une telle série est une somme de sinus ou cosinus de différentes périodes, phases et amplitudes.

Lisez cet article wikipédia pour en savoir plus.

Remarque très importante

Une décomposition en séries de Fourier se fait sur des fonctions périodiques. On fait donc l’hypothèse que les cours ont des composantes périodiques et une tendance. Attention : je n’ai pas enlevé la composante « tendance ». Ne faites pas l’impasse là-dessus au GO !

Par exemple, vous pouvez retirer des cours la moyenne mobile à 100 jours.

Fast Fourier Transform

Ainsi, les mathématiciens on construit des outils comme la FFT (Fast Fourier Transform). En effet, les transformées de Fourier permettent de transformer un signal (une courbe) en sa décomposition de Fourier.

Et cet outil est implémenté en langage Python

Le langage de Python est un langage très utilisé, le plus utilisé dans le mode, en fait. En plus, il est idéal pour la manipulation des données et les calculs scientifiques. C’est le langage de prédilection des data scientists mais aussi de l’IA et du machine learning.

Le Python permet de facilement manipuler des données comme des cours de bourse et calculer des choses à partir de ces cours. Alors, peut-il nous aider à prévoir les cours de bourse ?

La réponse est oui.

Dans le futur je vous ferai peut-être des cours sur Python, numpy, matplotlib et pandas, des librairies python très utiles. Mais pour l’instant nous allons utiliser ChatGPT.

Utiliser ChatGPT pour la décomposition en séries de Fourier

Ensuite, ChatGPT va être notre aide de camp, notre copilote pour développer en Python de quoi :

• télécharger des cours de bourse
• tracer des graphiques
• décomposer les cours de clôture en séries de Fourier
• construire une courbe calculable qui approcher les cours

En quoi cela peut nous être utile ?

Mais on pourrait se demander à quoi cela sert ?

Ne nombreux traders et data scientists aimerait pouvoir utiliser le machine learning, la data science et l’IA pour pouvoir prévoir les cours de bourse.

Une série de Fourier est une fonction calculable. Si on arrive à approcher les cours par une fonction calculable, peut-être qu’on peut prévoir les cours de bourse !?

La logique là-dessous, pour prévoir les cours de bourse avec les séries de Fourier

Ainsi, ce qui sous-tend l’intérêt que je porte à Fourier, c’est que :

• les cours de bourse sont faits de cycles et de tendances.
• Une tendance, si l’on regarde de plus près (caractère fractal du marché) est fait de cycles.
• On a donc des cycles, c’est-à-dire des périodes et fréquences.
• Or, les transformées de Fourier permettent de lister ces fréquences.

Par conséquent, un outil qui permet d’extraire du marché les fréquences qui le compose, c’est un outil extraordinaire.

Votre prochain sujet de Grand Oral de Maths ?

En fait, c’est un beau sujet de Grand Oral de Maths pour le Bac, non ?

En effet.

Je vais vous montrer comment créer votre dossier de Grand Oral grâce à Colab.

Pour voir tous mes articles liés au Grand Oral, cliquer ici.

Google Colab, un outil pour l’IA

Et on ne va pas ne pas se faire plaisir. On va utiliser une outil prévu pour de l’IA. Attention on entre dans la cours de grands.

Google Colab est un outil qui permet d’écrire des « notebooks ». Un notebook est une page HTML qui contient à la fois du code Python, du texte et des graphiques.

Le gros plus, c’est qu’on peut exécuter le code et afficher le résultat dans la même page.

Voici comment se présente un notebook.

En haut on a le code, puis le résultat de l’exécution du code, pour finir par un graphique généré par le code.

C’est un peu comme si on avait une calculatrice programmable dans un cahier.

Pour l’utiliser il faut un compte Google.

Bon, on commence ?

Demander à ChatGPT comment télécharger les cours de bourse

Au début il faut récupérer des cours de bourse. ChatGPT nous donne la réponse.

Créez un nouveau notebook dans GitLab.

Si vous voulez voir directement le résultat…

Dans le cas où vous seriez pressé, regardez la vidéo:

Comment récupérer le code complet dans GitHub ?

Si voulez passer les détails :

• créez-vous un compte GitHub.
• Cliquez sur ce lien.
• Cliquez sur le bouton Fork.
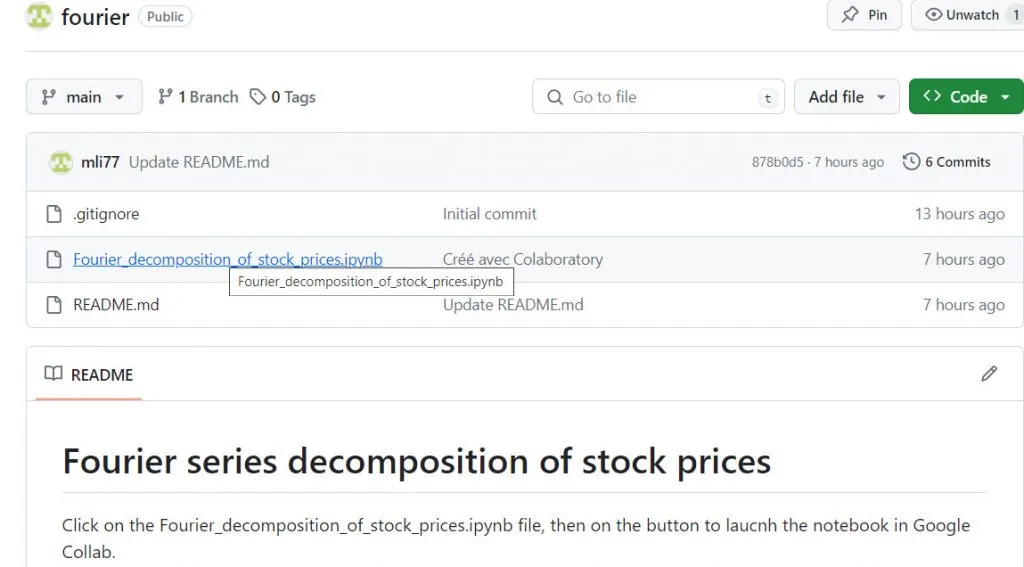
• Ensuite, cliquez sur le fichier notebook (voir ci-dessous).
• Au-dessus du fichier, cliquez que le bouton Open in Colab.

Puis, cliquer sur le notebook.

Et ouvrir le notebook dans Colaboratory.

Ajouter du code dans Colab

On ajoute du code en cliquant sur le bouton + Code ou sur ALT+Entrée (sur Windows). Remarque : on peut aussi ajouter du texte formaté avec le bouton + Texte.

Cela ajoute une cellule. Le code est organisé par cellules. Ainsi, une cellule est un ensemble de code exécutable via la flèche en haut à gauche de la cellule.

Exécuter des commandes non python dans Colab

Les premières instructions vont dire qu’il faut installer deux librairies python :

!pip install yfinance
!pip install matplotlib

Le point d’exclamation devant dit à Colab qu’il ne s’agit pas de python mais de commandes shell.

Après cela, cliquez sur la flèche pour exécuter la cellule.

Quelques mots sur le langage Python

J’espère pourvoir créer quelques tutoriels sur Python, enfin, si cela vous intéresse. Dites-le moi dans les commentaires. Mais ce que vous devez savoir sur ce langage, c’est que contrairement à d’autres, il n’utilise pas les accolades pour isoler les blocs d’instructions. Au contraire, il utilise des indentations.

Par conséquent, quand vous voyez des indentations, il faut les respecter, sinon votre code ne marchera plus !

Encore un mot : def indique une fonction. Une fonction ou méthode est un bout de code qui peut être appelé à différents endroits du programme.

Télécharger des cours de bourse pour le calcul des séries de Fourier

Ensuite, on va télécharger des cours historiques car c’est nécessaire pour la décomposition en séries de Fourier.

Voici le code

import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt

# Define the stock symbol and date range
stock_symbol = "AAPL"  # Replace with the desired stock symbol
start_date = "2022-01-01"
end_date = "2022-12-31"

# Download historical data
historical_data = yf.download(stock_symbol, start=start_date, end=end_date)

# Display the downloaded data
print(historical_data.head())

# Close
close_values = historical_data['Close'].values

# Plot the close values
plt.figure(figsize=(10, 6))
plt.plot(close_values, label='Close Values', color='blue')
plt.title('Stock Close Prices Over Time')
plt.xlabel('Date')
plt.ylabel('Close Price')
plt.legend()
plt.grid(True)
plt.show()

Exécutez ce code. Cela donne un beau graphique:

Attaquons la décomposition en séries de Fourier à proprement parler

Pour appliquer la transformée de Fourier sur les cours de clôture, nous allons utiliser des fonctions de la librairie python numpy. C’est une librairie importée par défaut dans Google Colab. En effet, elle est très utilisée par les data scientists.

Notre cher ChatGPT va nous pisser le code…

Le code

Voici le code :

import numpy as np
import matplotlib.pyplot as plt

# Function to decompose the close values using Fourier series
# Function to decompose the signal into sinusoidal components
def decompose_fourier(signal):
    n = len(signal)
    fft_values = np.fft.fft(signal)
    fft_freq = np.fft.fftfreq(n)

    # Keep only positive frequencies
    positive_freq_mask = fft_freq > 0
    fft_values = fft_values[positive_freq_mask]
    fft_freq = fft_freq[positive_freq_mask]

    # Sort frequencies and corresponding values by amplitude
    sorted_indices = np.argsort(np.abs(fft_values))[::-1]
    sorted_freq = fft_freq[sorted_indices]
    sorted_amplitude = np.abs(fft_values[sorted_indices])

    return sorted_freq, sorted_amplitude, fft_values, fft_freq

# Decompose close values using Fourier series
freq, amplitude, fft_values, fft_freq = decompose_fourier(close_values)

# Plot the amplitudes of different frequencies
plt.figure(figsize=(10, 6))
plt.plot(freq, amplitude, marker='o', linestyle='-', color='b')
plt.title('Fourier Decomposition of Close Values')
plt.xlabel('Frequency')
plt.ylabel('Amplitude')
plt.grid(True)
plt.show()

Mais qu’est-ce qu’une série ?

Tout d’abord, définissons ce qu’est une série. Rien à voir avec Netflix ! Une série c’est une somme de terme, les éléments de la série. mais cette somme est infinie. C’est-à-dire qu’il peut y avoir un nombre infini de termes dans la somme. On a donc une fonction Sn(x), fonction de x et de n, le nombre de termes. Et quand n tend vers l’infini, la série tend vers une limite, fonction de x.

Dans notre cas, Sn(x) quand n tend vers l’infini, c’est le cours de bourse réel.

Cela signifie qu’il faudrait, en théorie, un nombre infini de fréquences pour donner la valeur exacte du cours. On comprend qu’on en aura qu’une valeur approchée.

Lien avec les développements limités

En cours de Maths vous avez sans doute vu les développements limités. Un développement limité donne la valeur d’une fonction proche de x. C’est assez comparable dans la forme. Le sujet des séries est passionnant et l’on étudie la convergence (ou divergence) des séries…

Cependant, une série de Fourier est composée de sinus ou cosinus avec des fréquences (et des phases). Voyons cela de plus près.

Rendons les fréquences plus parlantes

La décomposition en séries de Fourier nous donne, par exemple, l’amplitude des fréquences trouvées. Bien sûr, les fréquence prépondérantes sont celles dont l’amplitude est élevée. Voir le graphique ci-dessous.

OK, c’et bien. Mais que peut-on faire de cela ?

Résumons.

La décomposition en séries de Fourier et ce qu’elle dit sur les cours de bourse

En fait, ce que nous avons obtenu, c’est un certain nombre de fréquences et leur amplitude. Plus l’amplitude est forte, plus cette fréquence est prépondérante dans les cours.

Afin d’être plus clair, je vais tenter d’expliquer. Supposons que les cours de bourse d’une action fassent un plus haut et un plus bas globaux (absolus) chaque année. C’est peu probable en réalité, mais admettons. Cela signifie qu’il y a des oscillations de période 1 an. Un peu comme la fonction sin(2pi.x/12)

La fréquence est l’inverse de la période. Soit :

1/12 mois^-1

J’espère que vous comprenez maintenant quand je parle de fréquence et de période.

Passons à la suite.

Reconstruire la courbe d’origine avec la série de Fourier

Ensuite, l’étape d’après est de reconstruire la courbe d’origine avec les séries de Fourier. Ainsi, vous l’avez certainement deviné, on va sommer les cosinus. Mais on ne va pas prendre toutes les fréquences. On ne va utiliser que celles qui ont les plus grosses amplitudes. Celle qui vont le plus influencer le résultat de la sommation. Encore une fois c’est ChatGPT qui va nous produire le code.

Le code

Cela nous donne le code suivant.

# Function to reconstruct the signal from sinusoidal components
def reconstruct_signal(freq, amplitude, n, fft_values, fft_freq, original_mean, original_diff):
    reconstructed_signal = np.zeros(n)
    for f, a in zip(freq, amplitude):
        phase = np.angle(fft_values[fft_freq == f][0])
        reconstructed_signal += a * np.cos(2 * np.pi * f * np.arange(n) + phase)

    # Adjust amplitude based on original range and add the mean value
    reconstructed_signal = (reconstructed_signal / np.max(np.abs(reconstructed_signal))) * (original_diff / 2) + original_mean

    return reconstructed_signal

# Reconstruct the signal using dominant frequencies
n = len(close_values)
original_mean = np.mean(close_values)
original_diff = np.max(close_values) - np.min(close_values)
reconstructed_signal = reconstruct_signal(freq[:10], amplitude[:10], n, fft_values, fft_freq, original_mean, original_diff)

# Plot the original and reconstructed signals
plt.figure(figsize=(10, 6))
plt.plot(close_values, label='Original Close Values', color='blue')
plt.plot(reconstructed_signal, label='Reconstructed Signal', linestyle='--', color='red')
plt.title('Original and Reconstructed Signals')
plt.xlabel('Time')
plt.ylabel('Close Values')
plt.legend()
plt.grid(True)
plt.show()

Ainsi on peut afficher une courbe qui approche les cours de bourse plus ou moins bien.

Les implications des séries de Fourier

Je ne sais pas si vous avez compris le truc important, là. On a trouvé une fonction (donc calculable) qui approche les cours de bourse. C’est génial ! Cela veut dire qu’on sait calculer les cours de bourse.

Mais uniquement dans le passé. Et pas super correctement;

Bien sûr, il n’est pas possible de prévoir les cours de bourse.

Néanmoins, on peut en déduire des indications :

• de tendance
• de sommets / creux.

Les traders ont l’habitude d’utiliser ce qu’ils appellent des indicateurs techniques pour détecter les tendances et les creux / sommets.

Alors essayons nous aussi. On va prendre des moyennes mobiles.

Définir des moyennes mobiles adaptées grâce au séries de Fourier

Ainsi, demandons à ChatGPT de nous créer des moyennes mobiles dont le paramètre (appelé longueur ou période) correspond à la fréquence de la série de Fourier. Ce que je veux c’est des moyennes mobiles dont la longueur correspond à la période équivalente aux fréquences de la série (p = 1/f).

ChatGPT écrit le code suivant

# Function to create moving averages for each dominant frequency
def create_frequency_ma(freq, n, original_data):
    mas = []
    for f in freq:
        period = int(1 / f)  # Calculate period based on frequency
        ma = np.convolve(original_data, np.ones((period,))/period, mode='same')
        mas.append(ma)
    return mas

# Reconstruct the signal using dominant frequencies
n = len(close_values)
original_mean = np.mean(close_values)
original_diff = np.max(close_values) - np.min(close_values)
reconstructed_signal = reconstruct_signal(freq[:10], amplitude[:10], n, fft_values, fft_freq, original_mean, original_diff)

# Create moving averages for each dominant frequency
mas = create_frequency_ma(freq[:10], n, close_values)

# Plot the original, reconstructed signals, and moving averages
plt.figure(figsize=(10, 8))
plt.plot(close_values, label='Original Close Values', color='blue')
plt.plot(reconstructed_signal, label='Reconstructed Signal', linestyle='--', color='red')
for i, ma in enumerate(mas):
    plt.plot(ma, label=f'MA for Freq {i+1}', linestyle='-.', alpha=0.7)

plt.title('Original, Reconstructed Signals, and Moving Averages')
plt.xlabel('Time')
plt.ylabel('Close Values')
plt.legend()
plt.grid(True)
plt.show()

Et voici le graphique. Notez qu’il y a des artefacts sur les moyennes mobiles.

Interprétation

Bon, passons les artefacts. Au centre du graphique on voit qu’il y a des moyennes mobiles qui sont pas mal du tout. La bleue du dessus indique une tendance plus long terme, décroissante. Je me suis arrêté là et je vous laisse le soin de continuer.

Pour votre sujet de Grand Oral

Si vous choisissez ce sujet pour le Grand Oral de Maths au Bac, voici les points forts que j’aimerais que vous reteniez :

• Nous avons analysé de caractère fractal des cours et l’avons canonisé sous forme d’une suite de fréquences.
• Nous en avons calculé une fonction capable d’approcher les cours.
• Mais cela ne marche que dans le passé. Et il est peut probable que cela marche sur les cours futurs.
• Par contre, on a une idée des cycles que connaît l’action et pouvons en déduire des indicateurs nous permettant d’analyser les cours de l’action dans le futur.

Pour aller plus loin

J’espère que cet article vous a plu. Si vous désirez plus de tutoriel sur Python, Numpy et leur usage en trading, dites-le moi dans les commentaires.

N’oubliez pas de regarder la vidéo pour voir tout cela en images qui bougent : lien.

Si vous souhaitez récompenser mon travail, vous pouvez sans doute acquérir mes Fiches du Trader Débutant à un prix modique. C’est une version en anglais (je vous fournis la version en Français sur demande).

Merci.

Illustrations : canva