Sujet de Grand Oral Bourse et Mathématiques
Sujet de Grand Oral portant sur les mathématiques et la bourse, recherché par élève de Terminale… Tel est le titre d’une annonce que j’aurais pu passer. J’ai eu des tas de demandes d’élèves de terminale qui ont prévu de passer leur Grand Oral en parlant de l’utilisation des mathématiques en bourse. Alors, voici comment je peux les aider.

Le Grand Oral c’est quoi ?
Table des matières
- 1 Le Grand Oral c’est quoi ?
- 2 Un sujet de grand oral lié à la bourse et aux mathématiques
- 3 Avertissement – Caveat Emptor
- 4 Mes conseils pour bien réussir la présentation de votre sujet de Grand Oral
- 5 Alors, ce sujet de Grand Oral ? Peut-on prédire les cours de bourse avec les mathématiques ?
- 6 Les cours de bourse s’analysent comme des ondes
- 6.1 Introduction
- 6.2 Les traders utilisent des graphiques avec des courbes
- 6.3 Les courbes de cours de bourse sont comme des signaux électriques
- 6.4 Comment rendre une courbe des prix en barres ou bougies continue et dérivable ?
- 6.5 Utilisation de la dérivée pour prédire dans certaines conditions le sens d’évolution des cours de bourse
- 7 Annexes pour le sujet de Grand Oral
- 8 Comment introduire plus de mathématiques dans votre sujet de Grand Oral ?
- 9 Comment aurait-on pu traiter autrement ce sujet de Grand Oral ?
- 10 Sujet annexe : Les mathématiques sont-elles indispensables dans le trading ?
- 11 La dernière ligne droite avant le Grand Oral
- 12 Si ce dossier vous a été utile…
Le Grand Oral est une des rares épreuves du BAC encore programmée en 2021. Elles sont peu nombreuses.
Regardez ma vidéo si vous préférez…
Nouveauté 2025 :
Ma vidéo ULTIME avec tous les sujets possibles pour le Grand Oral en maths sur la bourse…
Une des dernières épreuves du Bac
Il s’agit d’une épreuve du Bac ne durant pas plus de 20 minutes pendant laquelle l’élève de terminale présente un sujet. Puis il répond à des questions de ses professeurs adorés.
Le sujet doit porter sur des matières étudiées par l’élève en terminale :
- Mathématiques.
- Physique.
- Sciences Naturelles.
- Économie.
- Netflix…
Ah ! Désolé, la dernière est une activité extra-scolaire… 🙂
Pour voir tous mes articles liés au Grand Oral, cliquer ici.
Comment se passe l’épreuve du Grand Oral ?
Le futur bachelier présente pendant 5 minutes un sujet qu’il aura préalablement étudié pendant l’année.
Le sujet porte sur une ou deux spécialités choisies par l’élève.
L’épreuve est orale et se déroule devant des professeurs, par exemple, un professeur de la spécialité et un autre, comme un prof d’espagnol qui n’y connaît rien au sujet.
Ensuite le prof de Maths (par exemple) pose des questions plus techniques pendant 10 minutes. Cela peut être de faire une démonstration.
Ensuite, le candidat parle de son orientation et pourquoi il a choisi ce thème.
Le candidat au Bac a droit à des notes faites sur place.
Voilà. Si vous voulez en savoir plus, lancez-vous dans les méandres des sites de l’Éducation Nationale. Bonne chance.
Un sujet de grand oral lié à la bourse et aux mathématiques
Si certains futurs bacheliers présentent des sujets comme « La vie de la crevette en Amazonie concurrence-t-elle l’économie mondiale » ou « Un économiste a-t-il déjà prédit une crise financière grâce à la physique », beaucoup m’ont demandé de leur donner des pistes sur la bourse et les maths.
Du genre « Peut-on prédire les cours de bourse avec les mathématiques ? ».
Alors, j’ai décidé de rédiger un petit article sur ce genre de sujet.
Remarque 2024 :
Mon traitement de ce sujet n’est pas super académique. Si vous voulez un sujet plus académique, avec, en plus, un plan tout fait, reprenez le contenu de cet article ou de cette vidéo. Le sujet est « Comment simuler les cours de bourse avec les mathématiques ».
Avertissement – Caveat Emptor
Cela vous donnera l’occasion d’apprendre 2 mots d’anglais :-). J’aimerais vous mettre en garde.
Ne partez pas sur vos grands chevaux. Ne prétendez ABSOLUMENT PAS que l’on peut prédire les cours de bourse avec les mathématiques. Ce serait mal pris par les professeurs.
Je vais vous proposer ce qu’il faut révéler un peu plus loin.
Second avertissement :
- Faites le travail vous-même. La dernière fois que j’ai aidé ma fille en philo en proposant un peu de PNL et d’hypnose dans la dissertation, j’ai eu 9/20 !
Vous êtes en terminale, pas moi. J’ai eu 20/20 en Maths et Physique, mais je n’ai pas passé le Grand Oral ! Ok ?
Mes conseils pour bien réussir la présentation de votre sujet de Grand Oral
Attention, ce sont MES conseils. Pas forcément les meilleurs.
Ce que l’on veut voir en quelques minutes dans le Grand Oral c’est si vous savez vous exprimer en français de chez la France. En gros : grammaire et « est-ce qu’on vous comprend ». Savoir si vous êtes capable de vous faire comprendre sur un sujet un peu technique.
Et si vous avez retenu quelque chose des matières que vous avez suivies en même temps que vous regardiez Youtube.
Donc :
- Avant l’épreuve, chronométrez-vous. Entraînez-vous pour que cela tienne dans les temps sans que vous alliez trop vite. L’entraînement et le fait de savoir que cela tient, réduira votre stress.
- Soyez simple dans vos propos. Faites comme si vous expliquiez à mémé Jo. Le prof d’espagnol doit comprendre !
- Faites des phrases courtes.
- Utilisez des analogies et des métaphores (le cours de philo devrait vous avoir appris ce que c’est, c’est très utile, contrairement à la philo).
- Si possible, racontez une histoire : amenez vos examinateurs d’un point A à un point B.
- Faites comme si vous présentiez quelque chose et, avec un stylo, pointez un endroit. Ce, pour qu’ils ne s’endorment pas.
- Haussez de temps en temps la voix sur des passages importants. Cela les réveillera.
- Creusez les points présentés dans ce dossier sur le sujet de grand oral et entraînez, lors des questions, l’examinateur vers ces sujets que vous maîtrisez. Cela gagnera du temps, montrera votre maîtrise et évitera d’autres questions. Mais ne délayez pas trop ! Cela se voit quand on tergiverse et qu’on essaie de noyer le poisson.
- Répondez aux questions de façon précise et directe. En cas de difficulté, dessinez et utilisez des analogies.
- Au début de l’épreuve vous avez 20 minutes, je crois, pour écrive vos notes. Entraînez-vous pendant quelques jours avant l’épreuve du Grand Oral à écrive vos notes sur 2 feuilles de mémoire afin de les ressortir le jour J. Appliquez-vous et résumez votre thème en 2 feuilles que vous savez réécrire en moins de 20 minutes.
Alors, ce sujet de Grand Oral ? Peut-on prédire les cours de bourse avec les mathématiques ?
Vous vous souvenez de quand je vous parlais de la prédiction des cours de bourse et du danger de l’annoncer ? Non ? Alors c’est mal barré pour les études supérieures ! 🙂 Si oui, alors, je pense qu’il est plus prudent de dire que :
- Le trading est une activité spéculative en bourse. Certains traders utilisent des outils mathématiques simples leur permettant, dans certaines conditions et sur un laps de temps très bref, de suivre une tendance et, donc, d’avoir une forte probabilité de gain.
Par la suite, je mettrai en gras ce que vous pouvez reprendre dans votre présentation. Les titres qui suivent peuvent vous servir de plan.
Je ne garantis rien sur la réussite de votre GO. Je vais écrire cet article en quelques minutes. Ce n’est pas moi qui passe le Grand Oral… Faites votre job ! Je vous donne les indications et un plan possible.
Les cours de bourse s’analysent comme des ondes
Introduction
Les cours de bourse sont publiés sous la forme de cotation pendant une séance (journée de bourse). Une cotation c’est l’émission (sur un site web, par exemple) d’un prix. Ce prix est le prix auquel une ou plusieurs actions d’une même entreprise se sont échangées entre un acheteur et un vendeur.
Un trader va essayer de profiter du changement des prix pour acheter à un prix, et revendre plus cher.
Comment réussir à prédire l’évolution des cours ?
Les traders utilisent des graphiques avec des courbes
Les traders peuvent s’appuyer presque entièrement sur une discipline appelée Analyse Technique. Ce n’est pas le cas de tous, mais c’est mon cas.
L’Analyse Technique consiste à afficher des graphiques de cours de bourse et d’ajouter à la courbe des prix d’autres courbes calculées à partir des prix. On appelle ces courbes des Indicateurs Techniques. Certains sont prédéfinis et largement utilisés, comme le Stochastique, le MACD, le RSI ou la célèbre Moyenne Mobile.

Cliquer sur l’image pour zoomer.
Les traders utilisent des conditions (comme des croisements) sur les indicateurs pour savoir quand acheter ou vendre une action.
Ils peuvent également utiliser le chartisme, mais je n’en parlerai pas. Le lien avec les mathématiques est trop faible.
Les courbes de cours de bourse sont comme des signaux électriques
Un graphique de cours de bourse c’est comme la courbe d’une fonction, par exemple, qui représenterait l’évolution d’un courant électrique. Cette courbe est construite en relevant à intervalle régulier le cours de cotation de l’action.
Le problème, c’est que :
- cette courbe n’est pas continue quand on la représente avec des barres ou bougies (voir plus loin).
- Elle n’est pas dérivable : on ne peut pas calculer la pente de la courbe en chacun de ses points.

L‘axe du bas c’est le temps, les ordonnées c’est le prix de l’action.
Continuité
Habituellement, dans les journaux, les graphiques de prix sont représentés uniquement avec le cours de clôture. Ce qui donne une courbe comme celle ci-dessus dans le paragraphe précédent. Ou celle ci-dessous. Seule la clôture est représentée. Cette courbe est continue mais pas dérivable.

Barres et bougies : deux représentations très courantes mais pas continues
Mais, en réalité, les traders utilisent d’autres représentations comme celles-ci. Les plus courantes sont les barres et les chandeliers.

Les chandeliers ou bougies sont une façon de représenter les prix. Une séance c’est la journée de cotation. Il y a un cours d’ouverture (le premier cours du jour), le dernier (clôture), le plus bas et le plus haut du jour. Voir ci-dessous.

Deux représentations non continues
Or, avec ces représentations :
- Il n’y a pas qu’une valeur par abscisse (le temps est en abscisse), mais 3 ou 4.
- Il peut y avoir des sauts d’une barre ou chandelier à un autre, ce qui crée ce que l’on appelle un gap. Voir ci-dessous.

On n’a donc plus une représentation continue.
Rappel : ci-dessous, en haut, une courbe continue et (presque) dérivable.

Pas de continuité car un utilise les bougies ou les barres
Remarque : il est vrai que si l’on n’utilise que les cours de clôture, la courbe est continue. Mais dans la réalité, on n’utilise pas que les cours de clôture. C’est une notion importante à comprendre.
Ce qu’il faut surtout comprendre pour votre sujet de Grand Oral, c’est que :
- Les représentations des cours de bourse pour le trader ne sont habituellement pas continues (barres et bougies).
- Les gaps (sauts) sont très gênants pour les indicateurs techniques.
- Il faut donc une certaine « continuité » en se basant sur une valeur moyenne permettant de lisser ces gaps.
Nous allons voir un peu plus loin comment résoudre ce problème.
Dérivabilité
Si une courbe est dérivable on peut déterminer sa pente (son taux d’accroissement). C’est la première chose à faire pour espérer prévoir les cours de bourse.
Remarque : si la courbe présente des « angles », elle n’est pas dérivable (elle peut l’être à gauche ou à droite, mais cela n’aide pas trop le trader). Une moyenne mobile a moins d’angles (même si elle n’est pas réellement dérivable).

Or, pour analyser sérieusement les évolutions des prix d’une action, il faut pouvoir utiliser les mathématiques. Et le minimum à faire c’est de rendre la courbe continue et dérivable.
Nous verrons plus loin le chartisme qui n’utilise pas les mathématiques, mais c’est une pratique purement géométrique assez limitée.
REMARQUE IMPORTANTE : par dérivabilité, je veux dire « pseudo » dérivabilité; Faites attention en disant cela à un prof de maths. La moyenne mobile reste une courbe par segments de droites (on relie les points). Mais quand il y a beaucoup de points, et, de loin, elle est beaucoup plus lisse et « dérivable » que les prix. De plus, certains logiciels lissent la courbe et elle est alors plus dérivable encore.
Donc, dites bien qu’elle est « plus dérivable » que les prix, mais pas réellement dérivable (car arc brisé). Et cela permet de mieux tracer une tangente. Et la tangente donne la vitesse d’évolution des prix. C’est ce qui intéresse le trader.
Comment rendre une courbe des prix en barres ou bougies continue et dérivable ?
L’outil principal utilisé par les traders pour rendre la courbe des prix continue et dérivable est la moyenne mobile. C’est l’indicateur de base utilisé en Analyse Technique.
La moyenne mobile
On prend la somme des cours sur une période de N cotations et on divise par N. On recommence lors de la cotations suivante, et on obtient la moyenne des N derniers cours. Cette moyenne est glissante, car on recommence à chaque cours.

La formule est la suivante. Imaginons que chaque jour il y a un prix Pn. P0 est le prix du jour, P1 celui de la veille, P2 celui d’il y a deux jours.
Moyenne mobile sur N jours = (P0 + P1 + P2 + …. + PN-2 + PN-1) / N

Le lissage
La courbe obtenue avec la moyenne mobile est continue, lissée, et, la plupart du temps (mais ce n’est pas garanti), dérivable.
La courbe est lissée car le saut de la clôture de la veille à celle du jour a moins d’impact dans la moyenne, car on divise la variation de prix par le nombre de jours N. L’influence de la dernière variation de prix est divisée par N. Cela tasse les variations. Et, en moyenne, les cours oscillent autour d’une position… Moyenne.
Par contre, si les prix augmentent chaque jour de 1%, par exemple, cela sera pris en compte par la moyenne mobile qui va monter. Cette progression de la moyenne donnera naissance à un signal de tendance haussière.
Le bruit
En fait, la moyenne élimine (lisse) le bruit que constituent les variations quotidiennes des prix. Ce n’est que quand les jours à progression positive s’accumulent que la moyenne va indiquer une tendance haussière. On dit que la moyenne mobile est un filtre. Elle élimine le bruit qui n’est pas une tendance. Et laisse apparaître les tendances.
Reste à bien identifier ces tendances. Et pouvoir les mesurer.
La dérivabilité
On lisse avec des moyennes mobiles pour avoir des courbes continues, lisses, et, si possible, dérivables. Ensuite on étudie les tangentes : la dérivée, l’inflexion, la concavité et la convexité.
C’est un procédé approximatif. On n’arrive pas toujours à une courbe suffisamment lissée ou dérivable. Mais le trader va essayer d’utiliser l’indicateur (la moyenne) pour prédire l’évolution des cours.
Quand la moyenne change de direction, cela veut dire qu’il y a une tendance dans l’évolution des prix :
- Si la moyenne monte, les prix montent « en moyenne ».
- Si elle baisse, les prix baissent « en moyenne » .
Le trader va donc tracer (dessiner réellement ou mentalement) la tangente à la moyenne pour estimer visuellement sa pente.

Pourquoi la tangente et la dérivée ?
Il faut bien préciser dans votre sujet de Grand Oral, que les concepts de tangente et dérivée expliquent ce que tente de faire le trader. Mais, concrètement, il va utiliser cette notion au travers d’autres indicateurs, comme le ROC (Rate Of Change = taux d’accroissement). La dérivée sera calculée empiriquement et de manière approchée par un autre indicateur.
J’évoque la dérivée et la tangente uniquement pour arriver aux notions de convexité, de concavité et d’inflexion.
Pour arriver à cela, la moyenne mobile est l’outil de base pour dompter le bruit des cours de bourse et lisser les mouvements tout en détectant les tendances.
Utilisation de la dérivée pour prédire dans certaines conditions le sens d’évolution des cours de bourse
Quand une courbe est dérivable on peut tracer en chacun de ses points la tangente à la courbe. La pente de cette tangente représente le taux d’accroissement de la courbe : si ce taux vaut 2% cela veut dire que les prix vont, très localement, évoluer de 2%.
C’est exactement ce que recherche le trader.
Il va acheter l’action quand la pente de la tangente est positive et forte.
Convexité et concavité
Une courbe est dite convexe si le segment reliant deux de ses points est au-dessus de la courbe.

Si l’on prend la tangente, cela veut dire qu’une courbe convexe est au-dessus de ses tangentes.

Le contraire s’appelle concavité. Une courbe concave est sous ses tangentes.
Un point d’inflexion est un point où la courbe passe de convexité à concavité.
Indication : la concavité et la convexité se déterminent en calculant la dérivée de la dérivée. Une courbe convexe a une dérivée croissante.
Comment prévoir localement les cours de bourse ?
Le trader va donc regarder (soit visuellement, soit avec d’autres indicateurs) si la pente de la tangente est positive et croissante.
Dans ce cas, on a une assez forte probabilité que les cours continuent, pendant un court laps de temps, à progresser dans le même sens.

dans la même direction au-dessus de la tangente.
On peut donc, un court moment, considérer que, très probablement, les cours vont monter.
À la baisse, il suffit d’inverser les choses.
La réalité…
Pour que cela marche bien, il faut que la moyenne mobile soit suffisamment proche des cours. Or, ceux-ci ne sont pas toujours super sages (réguliers). Ils peuvent grandement varier. Le choix du paramètre N de la moyenne mobile est donc déterminant. Mais si les cours ont trop de dispersion, alors mieux vaut passer à une autre action plus « régulière ».
De plus, il faut que la hausse dure suffisamment longtemps. Ce n’est le cas, par exemple, qu’à un seul moment dans l’exemple ci-dessous.

En pratique, il faut prendre en compte plusieurs moyennes, avec différentes valeurs de N. Des petites et des grandes. Par exemple, ci-dessous, il y a deux situations claires où les différentes moyennes mobiles sont « alignés ». C’est encore mieux pour le trader. Mais c’est une autre histoire.

Des conditions à respecter
Attention : tout ceci n’est valable que sous certaines conditions.
- Les nouveaux prix doivent être assez proches les uns des autres (pas de gros gaps).
- La courbe des prix doit être assez lisse pour que la moyenne mobile soit dérivable.
- Rien ne garantit que les cours futurs vont respecter la convexité.
- Cela peut durer plusieurs jours ou très peu de temps.
- Il est très difficile de savoir jusqu’à quel prix les cours vont monter. Cela ne peut pas être déterminé. Le trader est condamné à suivre les cours de bourse.
- Les indicateurs techniques comme la moyenne mobile introduisent un retard par rapport aux cours que le trader doit prendre en compte.
Une discipline non déterministe
Le trading reste une discipline non déterministe. Cette technique reste une approximation. Rien n’est garanti.
On peut, dans certaines circonstances détaillées ici, avoir un idée de la direction et de la vitesse de l’évolution des cours, mais en aucun cas on peut, de façon déterministe, prévoir jusqu’où vont aller les cours.
Il existe bien des techniques chartistes pour le faire, mais elles n’ont rien de mathématique. Cela fait intervenir les statistiques, mais de façon très empirique.
Annexes pour le sujet de Grand Oral
Ce qui précède est déjà assez long à présenter en 5, voire 10 minutes. Mais je vais vous donner d’autres éléments, dont certains relatifs aux sciences physiques.
Une courbe est décomposable en ondes
C’est absolument hors programme, mais une courbe peut être approximée par une somme de sinusoïdes. Les calculs sont complexes et on aborde cela en prépa maths. Cependant, avec des indicateurs techniques on peut s’en approcher.
Le trader peut choisir d’étudier une de ces sinusoïdes en particulier. Il va rechercher les phases de cette courbe.
Les phases en bourse
Un trader célèbre, Stan Weinstein, a démocratisé l’idée de phase. Dans l’évolution des cours de bourse il y a souvent 4 phases :
- Stagnation sur un niveau bas.
- Hausse.
- Stagnation mais sur un niveau haut.
- Baisse.
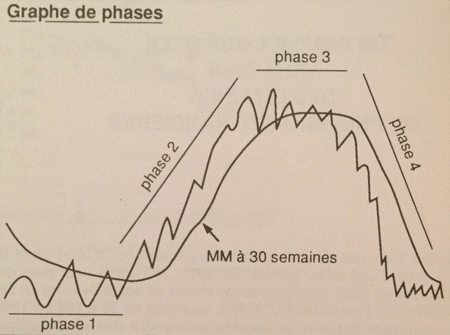
Sur chacune de ces phases, le trader peut utiliser la notion de tangente que nous avons vue, pour essayer de prédire dans quelle direction les cours vont aller.
En physique on peut comparer cela à un tir balistique :

Sujet de Grand Oral : les sciences physiques et la bourse
Abordons maintenant quelques idées et notions de sciences physiques.
La dérivée c’est la vitesse de progression des cours
Imaginons, un peu comme Einstein et son photon, que l’on soit un mobile en déplacement. La courbe des prix (on prendra la moyenne mobile qui en est une version continue et la plupart du temps dérivable) est sa trajectoire.
Plaçons-nous comme Einstein sur le dos de ce mobile. La pente de la tangente à la courbe est la vitesse du mobile.
La convexité indique que la vitesse augmente : c’est l’accélération.
Le trader cherche une vitesse de progression positive et forte, et, si possible, une accélération des cours.
Le momentum ou l’inertie
Imaginez un tir de canon. L’obus va monter. En physique, on a :
- Somme des forces = masse x accélération
On parle en mécanique d’impulsion ou de quantité de mouvement :
- masse x vitesse
En bourse, on recherche la vitesse de progression des cours (comme décrit dans le chapitre précédent), mais aussi une masse élevée. Mais, les cours de bourse n’ont pas de masse !
On parle de momentum…
Imaginez que beaucoup d’acheteurs se précipitent pour acheter une action. Cela va pousser les prix vers le haut. Cela correspond à une « somme des forces » élevée, et une impulsion masse x vitesse importante.

C’est la situation idéale pour le trader.
L’inertie – Comme un pétrolier
Le trader adore les tendances. Une tendance c’est comme une trajectoire quasi rectiligne. C’es l’idéal pour le trader.

L’inertie
Quand une action est en tendance et qu’il y a beaucoup de momentum, il faut beaucoup de force pour arrêter et inverser cette tendance. On dit que le mobile a de l’inertie.

En bourse cela peut être une information importante qui impacte le chiffre d’affaires de l’entreprise. Mais si rien de particulier n’est annoncé, les cours continuent d’aller dans la même direction.
J’utilise souvent l’analogie du pétrolier. Un pétrolier est un très grand navire qui a beaucoup d’inertie. Pour des manœuvres d’approche d’un port, il doit être assisté par des remorqueurs pour faciliter les changements de direction.
L’élastique et le retour à la moyenne
Une autre notion correspond à ce que l’on appelle en bourse, le retour à la moyenne ou mean reversion en anglais.
Cela signifie que plus les cours s’éloignent de leur position moyenne (la moyenne mobile), plus il y a de probabilité qu’ils reviennent à cette moyenne.

Conséquence : plus les cours sont éloignés de leur position moyenne, plus il y a de chances qu’ils y reviennent. Et qu’il la dépassent dans l’autre sens, comme une balançoire.
On peut donc utiliser l’analogie de l’élastique et du ressort. La force de rappel exercée sur les prix est du genre :
- F = k.l où l est l’élongation du ressort.
Cette force va « rappeler » les cours vers la position de repos : la moyenne.

J’ai peu travaillé sur un plan de sujet de grand oral bourse et physique. Je vous laisse le faire. Je suggère de partir de l’intro, de la nécessité de rendre les courbes de prix continues et dérivables, puis enchaîner sur les notions de physique.
Comment introduire plus de mathématiques dans votre sujet de Grand Oral ?
Enfin, pour introduire plus de Maths concrètes dans votre sujet, vous pouvez utiliser une fonction qui, tracée ressemble à des cours de bourse. Ensuite vous la dériverez (2 fois) et détecterez les points d’inflexion, la convexité, etc. Et vous appliquerez ce que l’on a vu.
Exemple de fonction pour votre Grand Oral :
- f(x) = (3cos(x)+3xsin(2x+2)+1.5x^0.5cos(7x+1)+27)/10
- ou, plus simple : f(x) = (3cos(x)+3sin(2x+2)+1.5cos(7x+1)+27)/5
Utilisez ce site pour la tracer : https://www.mathe-fa.de/fr
Comment aurait-on pu traiter autrement ce sujet de Grand Oral ?
Quand on parle de prévoir les cours de bourse on entend souvent ces deux choses :
- Utiliser une droite de régression.
- Ou les réseaux de neurones.
La régression est-elle utile pour prévoir les cours de bourse ?
Je n’ai pas parlé de régression car cela ne marche que quand il y a une tendance. Dans les autres cas, on se ramène à une courte période où il y a effectivement une tendance. Ce qui revient à utiliser la même méthode. La droite de régression est donc un peu comparable à notre tangente. D’ailleurs, souvent on ne calcule pas une droite de régression, mais une moyenne mobile spéciale.
Ce qui revient donc à peu près à ce que l’on a présenté.
Les réseaux de neurones et l’intelligence artificielle
J’ai traité ce sujet dans cet article. Déjà, c’est hors programme de terminale. Ensuite, c’est assez compliqué. Et cela ne marche pas. Mal barré pour un sujet de Grand Oral de Bac.
L’IA et les réseaux ne neurones sont assez efficaces pour repérer des formes. Mais dans le cas des cours de bourse il ne suffit pas de repérer quelque chose qui ressemble vaguement à un chat.
Ensuite, en IA on peut procéder de 2 façons :
- Soit on a des tas de données (le big data) ; mais ce n’est pas le cas en trading. Les historiques ne sont pas assez longs.
- Soit on travaille avec des experts du domaine. Dans ce cas on revient au point de départ.
Le retour de la tangente
Dans tous les cas on se ramène au problème de la tangente. Or, des outils mathématiques plus simples sont aussi (et plus) efficaces.
Pour l’anecdote, il est possible de coder des robots de trading avec des outils comme MT4. Mais, si le langage utilisé permet de traiter des outils mathématiques simples, il n’est pas suffisant pour remplacer l’œil du trader.
C’est pour cela que je n’ai pas parlé d’IA poru ce sujet de Grand Oral bourse et mathématiques.
Sujet annexe : Les mathématiques sont-elles indispensables dans le trading ?
Pour répondre à une question posée dans les commentaires, j’ajoute ce sujet de Grand Oral.
Les traders à l’ancienne
Le trading n’est pas nouveau. On dit que c’est un japonais il y a quelques siècles qui aurait inventé les chandeliers japonais pour prédire l’évolution du cours du riz…
Et il y a quelques décennies, les ordinateurs n’étaient pas répandus.
Les ancien traders se contentaient alors de tracer des lignes et des figures sur les graphiques. On appelle cela le chartisme.
Les principaux termes à connaître sont :
- Les résistances et supports.
- Les triangles, fanions, têtes épaules.
- Les canaux.
- Les break-out.
Les principaux patterns chartistes en un graphique
Il serait trop long d’aborder chacune de ces figures chartistes ici. En voici un résumé en graphique.

Dans la capture d’écran ci-dessous on a tracé des supports et résistances. Quand les cours les cassent on a des occasions d’achat ou de vente.
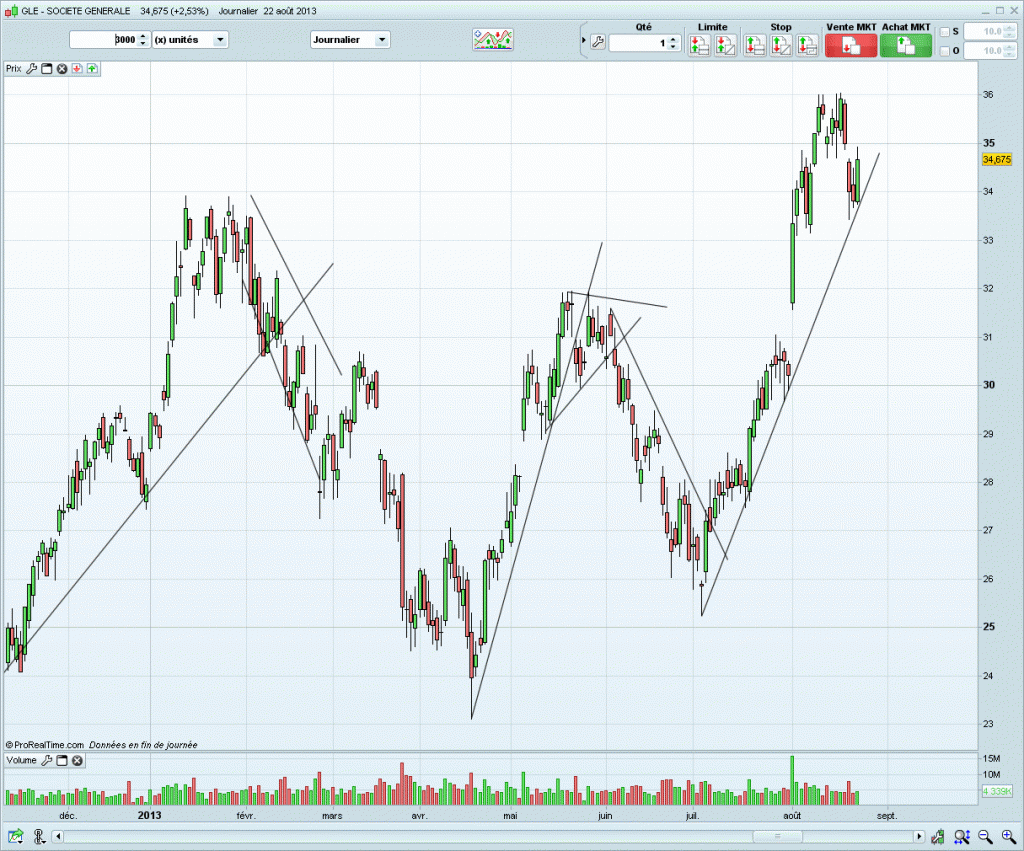
Il y a des figures (encore appelées patterns) plus compliquées que ces supports et résistances. Les puristes du chartisme vont même jusqu’à publier des statistiques de réussite de ces figures.
Il est donc possible de trader sans les mathématiques. Beaucoup de traders l’ont fait et le font encore.
Les mathématiques de plus en plus utilisées pour trader comme sujet de Grand Oral
La difficulté avec les méthodes graphiques et empiriques comme le chartisme, c’est que ce la ne fait pas très « pro » face à des investisseurs institutionnels qui placent des millions. Ce n’est pas non plus facile à automatiser.
Les maths c’est plus pour les professsionnels
D’autres techniques se sont donc développées, utilisant les mathématiques :
- Utilisation d’indicateurs techniques comme je le décrit plus haut – cela reste très basique.
- Utilisation d’équations différentielles, très utilisées pour pricer les options, comme la formule de Black & Scholes.
- Les différentes formes de régression.
- La data science pour analyser le sentiment de marché et l’intelligence artificielle avec, par exemple, les réseaux de neurones.
- L’électronique et des algorithmes qui vont très vite grâce à des cartes électroniques qui déclenchent des ordres et les annulent rapidement avant qu’ils soient passés afin de découvrir les intentions des autres traders et jouer contre eux. C’est le High Frequency Trading.
- Les arbitrages : des algorithmes qui détectent des incohérences entre le cours à New York d’une action son cours à Paris. On parle d’arbitrage.
Une réponse de normand
Un sujet comme celui-ci devrait, à mon avis, parler du chartisme. Mais préciser que l’utilisation des mathématiques permet d’aller plus loin et d’automatiser les trading.
Les professionnels, comme un certain trader qui aurait perdu des milliards pour une banque française il y a quelques années, utilisent des algorithmes pour gagner sur de toutes petites variations de cours mais avec de grosses sommes grâce à des modèles mathématiques. Les spécialistes qui écrivent et codent ces modèles s’appellent les Quants (pour Quantitative Analysts).
L’utilisation des mathématiques est donc plutôt une affaire de pros dans les grandes sociétés. Mais les particuliers font avec le chartisme ou chartisme plus indicateurs techniques.
Pros ou particuliers
Les professionnels ont des frais et besoins de couverture moindres, et des machines et réseaux plus rapides (ce qui compte pour la réussite d’un trade). Ils peuvent donc profiter de tous petits mouvements dans ce que l’on appelle le « bruit » du marché.
Les particuliers, eux, doivent profiter de tendances un peu plus longues car leurs frais sont plus importants.
Deux populations
Il existe donc deux populations :
- Ceux qui utilisent massivement les maths.
- Les particuliers, qui ne le font que très peu ou pas du tout.
Les maths ne sont donc pas indispensables pour trader.
Attention : certains professionnels ou néophytes prétendent que dans le monde actuel, la rapidité et les modèles mathématiques sont indispensables pour gagner. C’est une vision erronée. Il y a des tas d’exemples de particuliers qui réussissent avec une bonne méthode.
Mais faites attention à cela quand vous présentez votre sujet de Grand Oral.
La dernière ligne droite avant le Grand Oral
Faites en sorte de résumer tout votre sujet en 2 feuilles de papier. Apprenez-les par cœur et entraînez-vous à les reproduire de mémoire en moins de vingt minutes.
Chronométrez-vous pour votre oral. Récitez devant vos parents, des amis.
Tentez d’imaginer les questions qui peuvent être posées. Regardez les commentaires de cet article pour voir ce qui peut rester flou pour des gens. Et revoyez votre cours de maths ou physique pour les notions évoquées dans le sujet. J’ai posté un commentaire dans lequel je donne des idées de questions.
Si ce dossier vous a été utile…
Si ce dossier sujet de Grand Oral vous a aidé ou si vous l’avez apprécié :
- laissez un commentaire.
- Partagez sur les réseaux sociaux, les forums.
- Demandez à vos parents de m’acheter une petite formation, mon livre sur la gestion du temps ou de diffuser l’adresse de ce site à des amis et collègues passionnés de bourse.
J’ai publié une vidéo formation longue gratuite sur l’analyse technique. Visionnez-la !
Que la Force soit avec vous !
Illustrations : canva



Comments ( 94 )
Voir aussi commentaire voisin.
En ce qui concerne les outils mathématiques utilisés : moyennes mobiles. La dérivée c'est pour la théorie, mais en pratique, on trace à la main ou mentalement la tangente sur le graphique. Pour le calculer il faut utiliser de la régression (linéaire) pour obtenir une formule à partir des points relevés, chose qui n'est pas au programme. Le domaine est très très vaste. La question de "prévoir les cours de bourse" a été étudiée par nombre de matheux ! Je suis resté à un niveau très simple.
En réalité, parfois, sur le marché américain ou les cryptos, cela peut continuer. Mais si le trader entre sur un bond de 30%, il risque de perdre tout de suite 30% si les cours retombent. Or le trader n'aime pas le risque. Il faut donc que les bougies des cours de bourse ne fassent pas trop de gaps.
Vous n'avez pas besoin de parler de cela dans votre exposé. Mais si vous avez l'occasion de le placer dans la réponse à une question, cela fait gagner du temps.
Si l'on ajoute différentes suffisamment de différentes fréquences et déphasages, on peut construire une courbe d'a peu près n'importe quelle forme (sauf des créneaux parfaits).
Quand une radio reçoit une onde, l'onde est transformée en signal électrique et les informations contenues dans les différentes fréquence transporte la voix (FM veut dire modulation de fréquence : c'est en faisant varier la fréquence que l'on code la voix ou la musique). En trading, avec des indicateurs, on cherche à faire le contraire : on veut retrouver les différentes fréquences pures à partir du signal.
Autre analogie : un accord de guitare implique plusieurs cordes, plusieurs fréquences. En entendant le son on veut pouvoir retrouver les différentes cordes pincées.
Il peut demander la définition de la convexité et de la concavité. D'un point d'inflexion.
Savoir Savoir ressortir la formule de la moyenne mobile. Pour prendre un exemple si on vous le demande, vous pouvez dire que l'on peut approximer certains mouvements rapides et puissant à une parabole. x^2. Le calcul de la dérivée est simple.
Si j'étais prof de maths, je poserais ces questions sur la continuité, dérivée, convexité, concavité, tangente après avoir entendu cet exposé.
Révisez aussi les sinus et cosinus (savoir les tracer correctement et trouver leur dérivée) si vous en parlez.
Un prof un peu féru de la chose pourrait aussi parler de la régression linéaire. Il s'agit de trouver une courbe (et donc une fonction) qui approche le plus les points du graphique. La discussion / question peut déboucher sur la notion de barycentre. Une courbe de régression est celle qui minimise la distance de chacun de ses points au point du graphique boursier à la même date. Réviser la notion de barycentre et de distance. Mais cette question est plus improbable.
Il faut bien rappeler au jury que c'est une approche très simplifiée et valable seulement dans certaines conditions, sur un court laps de temps.
Soyez également prêt à expliquer ce qu'est une bougie ou un chandelier japonais, un gap, la structure des cours de bourse (le jour en abscisse, le cours en ordonnée, ou Open-close-high-low dans le cas des bougies). Pour quelqu'un qui ne connait pas du tout la bourse, ce n'est pas évident.
Vous pouvez aussi parcourir les questions posées dans les commentaires pour voir ce qu'un jury poserait comme question en dehors des maths. Pour moi tout cela est hyper évident. Mais pour une personne lambda, se représenter un graphique de cours de bourse c'est déjà difficile. Vous devrez faire preuve de pédagogie, montrer en dessinant dans l'air avec les mains, utiliser des analogies comme l'écran d'un oscilloscope ou un électrocardiogramme, ...
Une moyenne courte va indiquer le sens d'évolution des cour (vers le haut ou le bas, ou pas de sens clair) sur quelques jours seulement.
Une moyenne de 100 jours va indiquer la tendance (tendance d'évolution des prix) à moyen - long terme. On peut être en tendance haussière sur le moyen - long terme mais en tendance baissière sur quelques jours. On appelle cela, alors, une correction dans une tendance haussière. C'est un eu comme si les prix progressaient en dent de scie.
À partir de là, on peut décrire des signaux d'achat (par exemple un indicateur passe positif ou négatif). cela aide le trader qui, pour ceux qui font de l'intraday sur une unité de temps très courte comme 1 minute ou 10 sec, ont besoin d'agir vite.
Cette histoire de courbe dérivée, c'est un peu comme quand on pilote une formule 1. On peut se référer au défilement du paysage, à la vue des virages, mais le pilote a besoin du compte-tours et du compteur de vitesse pour savoir quand freiner, rétrograder, etc. Ce sont des "indicateurs" du nombre de tours moteurs, de la vitesse. Pourtant, la trajectoire est là... Mais on a besoin de ces indicateurs.
Une autre raison c'est aussi que les belles tendances longues ne sont pas si fréquentes que cela. Parfois les mouvement est indécis. Et on a besoin de plus d'informations. De même, certains traders entrent sur une forte hausse sans voir que l'action a perdu 80% dans les derniers mois. Cette forte hausse risque d'être très courte et d'être suivie par une nouvelle forte baisse. IL y a donc besoin d'une vision d'ensemble que le trader qui a la tête dans le guidon n'a pas toujours.
La dérivation est une introduction niveau terminale à l'analyse des signaux avec extraction des différents cycles contenu dans les graphiques, et qui nécessite des connaissances mathématiques plus avancées.
Ces indicateurs construits à partir de la moyenne mobile sont comme le GPS dans une voiture. Et la dérivée est là pour quantifier (donner une valeur) au potentiel de gain. Cela permet de construire des screeners (programmes de filtrage et de tri entre différentes acitons) qui trouvent les actions qui peuvent monter le plus fort.
Donc, on ne calcule pas la tangente. Par contre, on peut créer un autre indicateur qui va calculer le taux d'accroissement, qui correspond à la pente de la tangente. Par exemple, l'indicateur ROC. Mais je ne suis pas allé jusque-là. Cela devient compliqué.
un trader ne regarde pratiquement jamais une courbe de prix rien qu'avec les clôtures. Il utilise des bougies ou des barres donnant le plus bas, le plus haut, la clôture et l'ouverture. Cela fait 4 points pour une seule abscisse et les prix peuvent changer de quelques pourcents d'une barre à l'autre. La moyenne mobile peut se baser sur les cours de clôture, mais aussi sur (clôture + plus bas + plus haut)/3. De plus, faire la moyenne sur N barres tasse la volatilité des prix (les variations verticales sont amoindries : l'influence de la variation du prix d'un jour à l'autre est divisée par N).
Donc, les barres/bougies ne sont pas continues, mais la moyenne l'est. De plus elle est lissée et moins volatile.
Le trader veut une courbe plus lisse, dans laquelle les variations quotidiennes ont moins d'influence. Par contre, si les cours montent pendant plusieurs barres de suite dans le même sens, cela va se voir dans la moyenne (qui va se redresser). J'ai ajouté un paragraphe dans l'article pour préciser cela.